Lecture: 360.243 Numerical Simulation and Scientific Computing II, SS2022
Exercise 1
Handout: Thursday, March 10
Submission: Deadline for the group submission via TUWEL is Thursday, March 31, end of day
-
Include the name of all actively collaborated group members in the submission documents.
-
The binaries should be callable with command line parameters as specified below.
-
Submit everything (Makefiles, Shell-Scripts, Sources, Binaries, PDF with Plots/Discussion) as one zip-file per task.
-
TUWEL-Course: https://tuwel.tuwien.ac.at/course/view.php?idnumber=360243-2022S
General information
-
Use (and assume) the double precision floating point representation.
-
Test your MPI-parallel implementation on your local machine before you benchmark on the cluster.
-
Compare the results (i.e., residual and error) with your serial implementation to ensure a correct implementation.
-
Use only a small number of Jacobi iterations when benchmarking the performance your code: convergence is not required during benchmarking.
MPI-Parallel Stencil-Based Jacobi Solver
In this exercise, your task is to parallelize a stencil-based Jacobi solver for the 2D elliptic PDE
-\Delta u(x,y) + k^2 u(x,y) = f(x,y) \quad, \text{with} \ k=2\pi
for the "unit square" domain
\Omega = [0,1] \times [0,1]
with the analytic solution
u_p(x,y) = \sin(2\pi x) \sinh(2\pi y)
and right-hand-side
f(x,y) = k^2 u_p(x,y)
by implementing an MPI-based domain decomposition. The PDE is discretized on a regular finite-difference grid with fixed (Dirichlet) boundary conditions:
\begin{align}
u(0,y) &= 0 \\
u(1,y) &= 0 \\
u(x,0) &= 0 \\
u(x,1) &= \sin(2\pi x)\sinh(2\pi)
\end{align}
The second-order derivates are discretized using a central difference scheme resulting in a "5-point star-shaped stencil". As a staring point for your implementation, you can use your own serial implementation of the Jacobi solver from the NSSC I exercises or use the source-code distributed with this exercise (solver.hpp).
Domain Decomposition
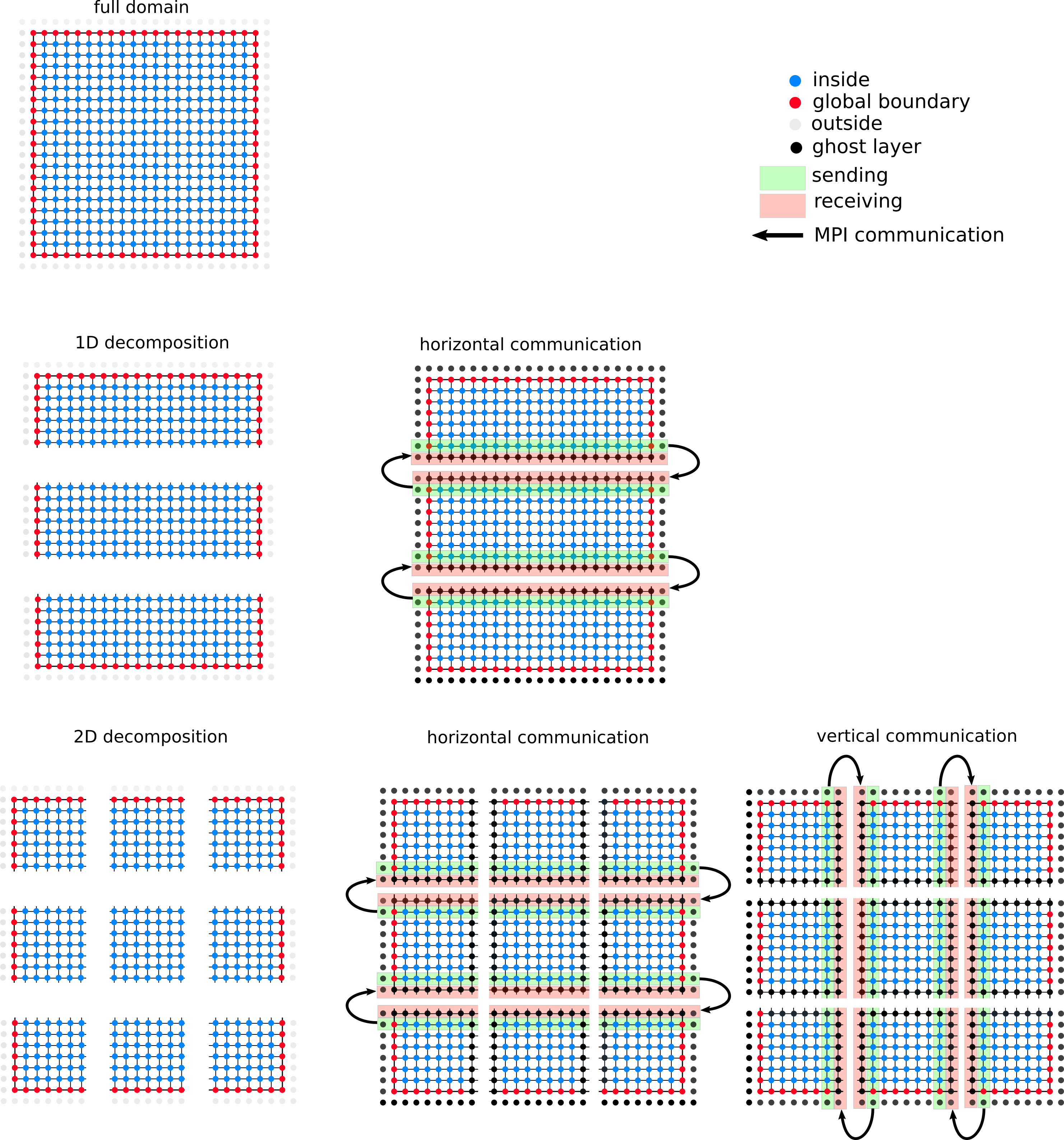
Your task is to decompose the finite-difference grid into domain regions such that multiple MPI-processes can independently perform an iteration on each region. The decoupling of the regions is achieved by introducing a ghost layer of grid points which surrounds each region. The values in the ghost layer of a region are not updated during an iteration.
Instead, after an iteration is finished the updated values for the ghost layer are received from the neighboring regions, and the boundary layer is sent to the neighboring regions (see Figure below).
Task 1: Questions (3 points)
- Describe the advantages/disadvantages of a two-dimensional decomposition (compared to a one-dimensional decomposition).
- Discuss if the decomposition of the domain changes the order of computations performed during a single Jacobi iteration (i.e., if you expect a numerically identical result after each iteration, or not).
- A generalization of the ghost layer approach would be to set the width of the ghost layer that is exchanged as a parameter
Wof the decomposition. This allows to performWindependent iterations before a communication of the ghost layers has to happen. Comment in which situation (w.r.t the available bandwidth or latency between MPI-processes) multiple independent iterations are potentially advantageous. - Assume a ghost layer with width
W=1(this is what you will later implement) and discuss if a data exchange between parts of the domain which are "diagonal neighbors" is required (assuming a "5-point star-shaped stencil"). - How big is the sum of all L2 caches for 2 nodes of the IUE-cluster link
Task 2: One-Dimensional Decomposition (4 points)
Your task is to implement a one-dimensional decomposition using a ghost layer and MPI-communication to update the ghost layers. Create a program which is callable like this:
mpirun -n NUMMPIPROC ./jacobiMPI resolution iterations
# example call
mpirun -n 4 ./jacobiMPI 250 30
NUMMPIPROC: number of MPI-processes to launchresolution: number of grid points along each dimension of the unit square; the grid spacing ish = 1.0/(\text{resolution}-1)iterations: number of Jacobi iterations to perform
Further and more specifically, your program should
- use
\bar{u}_h=\mathbf{0}as initial approximation tou, and (after finishing all iterations) - print the Euclidean
\parallel \cdot \parallel_2and Maximum\parallel \cdot \parallel_{\infty}norm of the residual\parallel A_h\bar{u}_h-b_h \paralleland of the total error\parallel \bar{u}_h-u_p \parallelto the console, - print the average run time per iteration to the console, and
- produce the same results as a serial run.
Finally, benchmark the parallel performance of your program jacobiMPI using 2 nodes of the IUE-Cluster for 4 different resolutions=\{125,250,1000,4000\} using between 1 and 80 MPI-processes (NUMMPIPROC).
More specifically, you should
- create a plot of the parallel speedup and a plot of the parallel efficiency for each
resolution, and - discuss your results in detail.
Notes:
- On your local machine, you can also launch MPI-runs using mpirun (after installing MPI, see
Makefilefor install commands on Ubuntu) - An example of a ”MPI”-Makefile and of a job submission script are provided with this exercise.
- The use of
MPI_Cart_create,MPI_Cart_coords, andMPI_ Cart_shiftfor setup of the communication paths is recommended. - Your implementation should work for any positive integer supplied for
NUMMPIPROC(e.g., 1,2,3,4,...) and also utilize this number of processes for the decomposition.
Task 3: Two-Dimensional Decomposition (3 points)
Extend your program from Task 2 by implementing a two-dimensional decomposition using a ghost layer and MPI-communication to update the ghost layers. Create a program which is callable like this:
mpirun -n NUMMPIPROC ./jacobiMPI DIM resolution iterations
# example call
mpirun -n 4 ./jacobiMPI 2D 125 200
- the command line parameters have the same meaning as above in Task 2
- the new parameter
DIMhas two valid values1Dor2Dand switches between one-dimensional and two-dimensional decomposition.
Ensure a correct implementation by comparing your results to a serial run. Benchmarking on the cluster is not required.
Notes:
- Your implementation should work for any positive integer supplied for NUMMPIPROC (e.g., 1,2,3,4,...) and also utilize this number of processes for the 2D decomposition.
- If a the 2D composition is not possible with the supplied number of processes (i.e., a prime number), your program should resort to a 1D decomposition.
Working with the IUE-Cluster
Connecting
- Your login credentials will be provided via email.
- You need to enable a "TU Wien VPN" connection.
- You can login to the cluster using
sshand your credentials. - You will be asked to change your initial password upon first login.
File Transfer
- You can checkout this git-Repository once you are connected to the cluster.
- You can transfer files and folders between your local machine and the cluster using
scp - All nodes of the cluster operate on a shared file system (all your files on the cluster are also available when executing jobs)
Compiling on the cluster
- The cluster has a login node (the one you
sshto, details will be announced in the email with the credentials) - This login node must only be used to compile your project and never to perform any benchmarks or MPI-runs (beside minimal lightweight tests of for the MPI configuration)
- All other nodes of the cluster are used to run the "jobs" you submit.
- To support cluster users, a set of environment modules (relevant for us is only the "MPI"-module) is made available. You can list all modules using
module avail - Note that you also need to load the modules you require in your job submission scripts (see example provided in this repo).
Executing jobs on the cluster
- Once you successfully compiled your program on the login node of the cluster, you are read to submit jobs.
- On our cluster job submissions are handled by the workload manager
SLURM(a very common choice). - A job essentially is a shell-script which contains a call of your executable (see examples in this repo)- A additionally a job-script specifies its demands w.r.t. to resources, e.g.
- how many nodes are required?
- which runtime is anticipated?
- how many MPI-processes should be launched on each node?
- After you submitted the job, it is up to the
SLURMscheduler to queue it into the waiting list and to inform you once the job has completed. - The "results" of your job are
- Potential output files which your program produced during execution.
- The recording of the stdout and stderr which was recorded while your job executed (e.g.,
slurm-12345.out)
Useful Resources
SSH: https://phoenixnap.com/kb/ssh-to-connect-to-remote-server-linux-or-windows
SCP: https://linuxize.com/post/how-to-use-scp-command-to-securely-transfer-files/
SLURM: https://slurm.schedmd.com/quickstart.html
Environment Modules: https://modules.readthedocs.io/en/latest/